Description Eulérienne
Les hypothèses de continuité (milieu et transformation) imposent que les
fonctions ![]() soient des bijections de la
configuration de référence
soient des bijections de la
configuration de référence ![]() sur la configuration actuelle
sur la configuration actuelle ![]() . Cette bijectivité impose
l'existence d'une relation inverse entre les variables de position de référence et les
variables de position actuelle. On a donc :
. Cette bijectivité impose
l'existence d'une relation inverse entre les variables de position de référence et les
variables de position actuelle. On a donc :
![]()
On constate donc qu'il est possible de changer de variables spatiales. La
description dite eulérienne consiste à considérer les variables ![]() et t comme indépendantes et à les
utiliser sous forme de "variables ou coordonnées d'Euler".
et t comme indépendantes et à les
utiliser sous forme de "variables ou coordonnées d'Euler".
Dans la description eulérienne, on ne se préoccupe pas de savoir ce qu'il advient de chaque particule. En fait on étudie ce qui se passe, à chaque instant, en chaque point de l'espace.
On peut exprimer la vitesse et l'accélération en fonction des variables d'Euler :
vecteur vitesse :
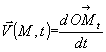
avec ![]()
vecteur accélération :
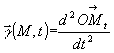
avec ![]()
Pratiquement, on peut dire qu'en description lagrangienne, on suit le domaine dans son mouvement, alors qu'en description eulérienne, on observe l'évolution du système en un point géométrique fixe pour l'observateur.