Imaginons que l’on connaisse un tenseur symétrique, à coefficients réels, par ses composantes dans la base principale :

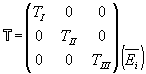
Considérons un vecteur unitaire quelconque :

On peut alors calculer le vecteur obtenu dans la direction  :

Dans la base principale, les composantes de ce vecteur sont :

        avec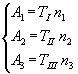   

D’autre part, comme le vecteur est unitaire nous avons :

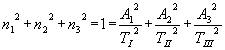
Nous constatons ainsi que les composantes du vecteur peuvent très bien représenter les coordonnées d’un point A dans l’espace des vecteurs propres. Avec l’équation précédente, on peut dire que le lieu décrit dans l’espace des vecteurs propres est un ellipsoïde, appelé ellipsoïde de Lamé.

Cette première représentation graphique tridimensionnelle permet de constater que les valeurs propres représentent les valeurs extrèmales de l’état tensoriel.

Ainsi dans le cas du tenseur de déformation, la plus grande dilatation linéaire et la plus petite en un point donné, sont données par deux des déformations principales , et .  

Par contre cette représentation de l’état tensoriel présente l’inconvénient d’être tridimensionnelle et donc peu aisée à dessiner. Il est possible d’obtenir une repésentation plane en considérant le plan formé par les deux vecteurs et . Ce plan présente généralement une intersection avec le plan orthogonal au vecteur . On désigne par la projection du vecteur sur le vecteur , par le vecteur obtenu par projection du vecteur sur son plan othognal. On a, avec des notations évidentes :

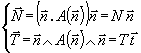        avec vecteur normal et vecteur tangent.

Suppons que le vecteur appartienne au plan principal formé par les vecteurs , et qu’il présente un angle avec la direction principale . On peut donc écrire :

        et    

Avec les formules de changement de base, il est facile de démontrer que l’on a :

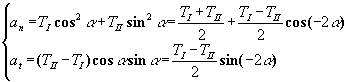
On constate donc que dans le plan vectoriel , lorsque l’angle varie, l’extrémité du vecteur parcourt un cercle dont le centre a pour coordonnées. Le rayon du cercle est . Le point extrémité décrit le cercle en sens inverse et du double de l’angle de position . Le cercle ainsi obtenu est appelé cercle de Mohr dans le plan principal . On conçoit aisément qu’il soit ainsi possible de construire trois cercles. La figure obtenue montre ainsi le tricercle de Mohr de l’état tensoriel.

A partir de la représentation de Lamé, on peut déduire que pour une direction unitaire quelconque, l’extrémité du vecteur doit se trouver à l’intérieur du tricercle. Les valeurs propres formant le diamètre de plus grand des cercles de Mohr sont les valeurs extrémales du vecteur normal. Leur différence constitue la plus grande valeur du vecteur tangent.